Question

A rectangular piece of plywood has a diagonal that measures three times the width. The length of the plywood is three feet more than the width. What is the length of the plywood’s diagonal? Round to the nearest tenth._____feet

Answer 1

Step 1. We start by making a diagram:

In the following image we have a diagram of the situation:

Step 2. We will label the with as "w", and since the diagonal is three times the width it will be labeled as "3w". Also, since the length is three feet more than the width, the length will be labeled as "w+3". This is shown in the following image:

Note that a right triangle is formed between the width, the length, and the diagonal:

Step 3. We can apply the Pythagorean theorem:

`(leg1)^2+(leg2)^2=(hypotenuse)^2`

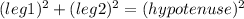
Where leg 1 is the width, leg 2 is the length and the hypotenuse is the diagonal:

`w^2+(w+3)^2=(3w)^2`

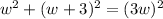
To find the length of the diagonal, we need to find w first.

To continue solving by applying the binomial squared formula:

`(a+b)^2=a^2+2ab+b^2`

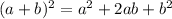
We apply it to (w+3)^2 and we get:

`(w+3)=w^2+6w+9`

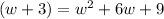
Substituting this into the Pythagorean theorem:

`w^2+w^2+6w+9^{}=(3w)^2`

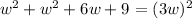
Next, on the right-hand side we solve the exponent:

`w^2+w^2+6w+9^{}=9w^2`

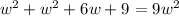
Step 4. Once we have applied the Pythagorean theorem and we have solved the operations in the resulting expression, we continue solving for w by subtracting 9w^2 to both sides and thus equating the expression to 0:

`w^2+w^2+6w+9-9w^2=0`

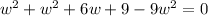
We add the like terms (the terms that contain w^2):

`-7w^2+6w+0=0`

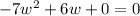
Step 5. Use the quadratic formula to solve for w:

`w=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Where a is the coefficient of the w^2 term:

`a=-7`

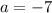
b is the coefficient of the w term:

`b=6`

and c is the independent term:

`c=9`

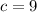
Substituting and solving the quadratic formula:

`w=\frac{-6\pm\sqrt[]{6^2-4(-7)(9)}}{2(-7)}`
`w=\frac{-6\pm\sqrt[]{36^{}+252}}{-14}`
`w=\frac{-6\pm\sqrt[]{288}}{-14}`
`w=(-6\pm16.97)/(-14)`

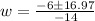
Next, we find one solution by using the + sign and another solution by using the - sign:

`\begin{gathered} w=(-6+16.97)/(-14)=(10.97)/(-14)=-0.78 \\ w=(-6-16.97)/(-14)=(-22.97)/(-14)=1.64 \end{gathered}`

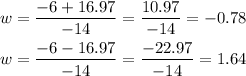
One solution is negative and one solution is positive. We will keep the positive solution since a width cannot be negative:

`w=1.64`

Step 6. The last step is to find 3w to find the length of the diagonal:

`3w=3(1.64)=4.92`

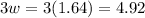
Rounding to the nearest tenth:

`3w=4.9`

Answer: 4.9 feet.