Question

Which of the following do we NOT know to be true?

Answer 1

The operator used in all the letters means that we should create a composite of the functions. This means that to find the composite of g(h(x)) we need to replace the expression variable x on the function g(x) by the expression for h(x).

The composite of a function by its inverse can be canceled, we will return to the same place. Therefore we can analyze each option and determine which one is the correct answer.

For option A we have:

`(f\circ f^(-1)\circ h)(x)=4`

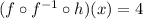
Since we have a composition of f with its inverse f^-1, then we can cancel these two terms and the result should be equal to the expression for h(x), which is equal to 4. Therefore the first option is true.

For option B, we have:

`(g\circ h\circ f^(-1))(x)=16+4\sec 4`

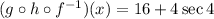
For this option we have a compositve of the functions g, h and the inverse of f. The problem is we don't know the expression for f or for its inverse, therefore we can't evaluate if this option is true or not. The correct answer is B.