We need to find the maximum and minimum points on [-2,1] for the function
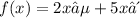
Then
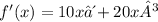
Now to find the critical points we have that
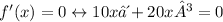
so
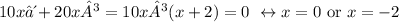
We get that we have two critical points at the interval [-2,1].
Now, to determine if they are minimum or maximum points we choose any point before and after them. We will choose -3,-1,1.
So,
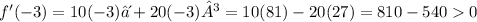

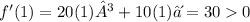
We should notice that f'(-3)>0 f'(-2)=0 and f'(-1)<0. Then

Moreover, since f'(-1)<0 f(0)=0, f'(1)>0. Then
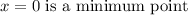
(a) We have that x=-2 is a maximum point and x=0 is a minimum point on the interval [-2,1]
To find the intervals where the function increase and decrease, notice that

since f'(x) is a continuous polynomial and f'(-2)=0 and f'(-3)>0.
Now,
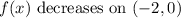
since f'(-2)=0 and here attaches a maximum, then the function needs to decrease until the nex critical point that is the point x=0.
After taking the minimum point x=0, f(x) will increase, i.e.
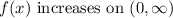
(b) f(x) increases on (-infinity,-2), decreases on (-2,0) and increases once more time on (0,infinity)
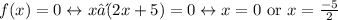
So,