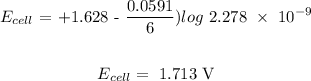Answer:
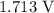
Step-by-step explanation:
Here, we want to calculate the standard reduction potential
Using the table of standard reduction potential, we have it that:
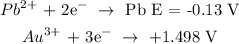
We have the value of E as:
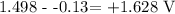
Now, let us calculate the value of Q, we have that as:
![Q\text{ = }\frac{[Pb^(2+)]\placeholder{⬚}^3}{[Au^(3+)]\placeholder{⬚}^2}\text{ = }(0.00120^3)/(0.871^2)\text{ = 2.278 }*\text{ 10}^(-9)](https://img.qammunity.org/2023/formulas/chemistry/college/gmn81bamax46v3825iqjlhc5v1d372a4jb.png)
Mathematically:
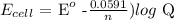
where n is the number of electrons transferred is 6
Substituting the values: