Given data:
* The force acting on the wire is 15 N.
* The length of the wire is 10 m.
* The extension of the wire is 0.1 mm.
* The young modulus of the wire is,

Solution:
The Young modulus of the metal wire in terms of area of the wire is,
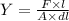
where F is the force acting, l is the length of wire, dl is the extension of the wire, and A is the area of the wire,
Substituting the known values,
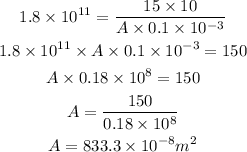
As the area of wire is same as the area of the circle.
Thus, the area of the wire in terms of the radius of wire is,
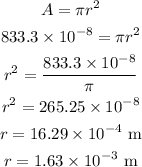
The diameter of the wire is,
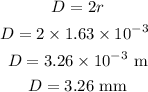
Thus, the diameter of the wire is 3.26 mm.