Question

A load of 15N produces an extension of 0.10mm in A metal wire 10m in length. If young modulus of metal is 1.8 x 10^11Pa Calculate the diameter of the wire

Answer 1

Given data:

* The force acting on the wire is 15 N.

* The length of the wire is 10 m.

* The extension of the wire is 0.1 mm.

* The young modulus of the wire is,

`Y=1.8*10^(11)Pa^{}`

Solution:

The Young modulus of the metal wire in terms of area of the wire is,

`Y=(F* l)/(A* dl)`

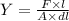
where F is the force acting, l is the length of wire, dl is the extension of the wire, and A is the area of the wire,

Substituting the known values,

`\begin{gathered} 1.8*10^(11)=(15*10)/(A*0.1*10^(-3)) \\ 1.8*10^(11)* A*0.1*10^(-3)=150 \\ A*0.18*10^8=150 \\ A=(150)/(0.18*10^8) \\ A=833.3*10^(-8)m^2 \end{gathered}`

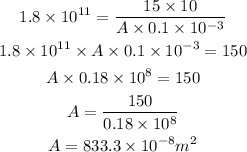
As the area of wire is same as the area of the circle.

Thus, the area of the wire in terms of the radius of wire is,

`\begin{gathered} A=\pi r^2 \\ 833.3*10^(-8)=\pi r^2 \\ r^2=(833.3*10^(-8))/(\pi) \\ r^2=265.25*10^(-8) \\ r=16.29*10^(-4)\text{ m} \\ r=1.63*10^(-3)\text{ m} \end{gathered}`

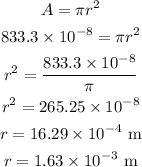
The diameter of the wire is,

`\begin{gathered} D=2r \\ D=2*1.63*10^{-3^{}}\text{ } \\ D=3.26*10^(-3)\text{ m} \\ D=3.26\text{ mm} \end{gathered}`

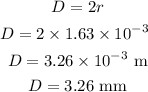
Thus, the diameter of the wire is 3.26 mm.