First, we have to find the acceleration of the car with the following formula.
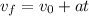
Where vf = 0, v0 = 84.21 km/h, and t = 9.260 s. Let's use these values and solve for a.
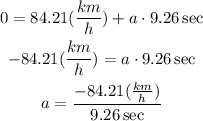
Before we divide, we have to express the speed in meters per second. We know that 1 km equals 1000 meters, and 1 hour equals 3600 seconds.
![\frac{84.21\operatorname{km}}{h}\cdot\frac{1000m}{1\operatorname{km}}\cdot(1h)/(3600\sec )\approx23.39((m)/(s))]()
Then, we use the transformed speed to find the acceleration.
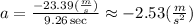
Once we have the acceleration, we can find the net force using Newton's Second Law.
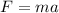
Where m = 1,052 kg and a = - 2.53 m/s2.
![F=1052\operatorname{kg}\cdot(-2.53((m)/(s^2)))=-2661.56N]()
Therefore, the net force is 2661.56 Newtons.
The negative sign indicates that the force applied is developing a negative acceleration on the car.