The formula to calculate the monthly payment is:
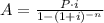
Where, A = payment amount per period (monthly)
P = Loan amount
r = interest rate per period
n = total number of payments
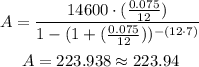
Monthly payments of $223.94
Now to calculate the total interest that will be paid during the term of the loan, We first have to calculate the final amount that is going to be paid:

The interest is the difference between the initial amount of the loan and the final amount (Fa) that is going to be paid.
Note that the interest rate and the time must be in the proportion, in this case 7 years and the interest rate is 7.5% annual.
Total interest $9622.