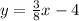Let's re-arrange the equation in slope-intercept form, which is y = mx + b.
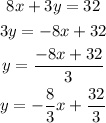
The line that is perpendicular will have a slope that is negative reciprocal of the slope of this line.
The slope of this line is -8/3.
Hence, the negative reciprocal of -8/3 is 3/8.
The choices are:
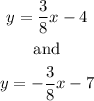
The first one is the line perpendicular since its slope is 3/8.
Answer