Question

Find hacks and round to the nearest 10th of a degree

Answer 1

`x=64.1`

Step-by-step explanation:

Step 1. The first step is to find the missing side of the triangle using the Pythagorean theorem:

In this case:

`\begin{gathered} c=16 \\ b=7 \end{gathered}`

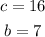
and we need to find a.

Substituting c and b into the Pythagorean theorem formula:

`16^2=a^2+7^2`

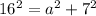
Solving for a:

`\begin{gathered} 16^2-7^2=a^2 \\ 256-49^{}=a^2 \\ 207=a^2 \\ \downarrow \\ \sqrt[]{207}=a \end{gathered}`

Step 2. The triangle now is:

And to find angle x we use:

`\begin{gathered} \\ \boxed{\sin x=\frac{\text{opposite side}}{hypotenuse}} \end{gathered}`

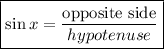
Substituting the known values:

`\begin{gathered} \sin x=\frac{\sqrt[]{207}}{16} \\ \end{gathered}`

Step 3. Solving for x:

`\begin{gathered} \sin x=\frac{\sqrt[]{207}}{16} \\ \downarrow \\ x=\sin ^(-1)(\frac{\sqrt[]{207}}{16}) \end{gathered}`

Step 4. Solving the operations:

`\begin{gathered} x=\sin ^(-1)(0.899218) \\ \downarrow \\ \\ x=64.05552 \end{gathered}`

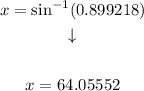
Rounding to the nearest tenth (1 decimal):

`x=64.1`

Answer:

`x=64.1`