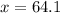Answer:
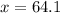
Step-by-step explanation:
Step 1. The first step is to find the missing side of the triangle using the Pythagorean theorem:
In this case:
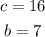
and we need to find a.
Substituting c and b into the Pythagorean theorem formula:
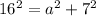
Solving for a:
![\begin{gathered} 16^2-7^2=a^2 \\ 256-49^{}=a^2 \\ 207=a^2 \\ \downarrow \\ \sqrt[]{207}=a \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/f73uu36ii5rnxtd9irt8xogrs5ih8d0c8r.png)
Step 2. The triangle now is:
And to find angle x we use:
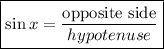
Substituting the known values:
![\begin{gathered} \sin x=\frac{\sqrt[]{207}}{16} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7kxq3ype9h6fraxl211zrsbjhptk3aooio.png)
Step 3. Solving for x:
![\begin{gathered} \sin x=\frac{\sqrt[]{207}}{16} \\ \downarrow \\ x=\sin ^(-1)(\frac{\sqrt[]{207}}{16}) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4k8sb7zoau22mqfzkwlbv69ga6ogje1pj0.png)
Step 4. Solving the operations:
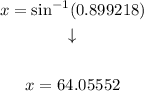
Rounding to the nearest tenth (1 decimal):
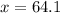
Answer: