When we have two roots of the same kind being multiplied, we can put them together, like this:
![\sqrt[3]{2x^5y^5}\cdot\sqrt[3]{16x^3y^7}=\sqrt[3]{2x^5y^5\cdot16x^3y^7}](https://img.qammunity.org/2023/formulas/mathematics/college/dxz0itts5a2z1pvykmhdnevbn2x9xo2cuh.png)
Now, we can reorder the factors so that we pair the numbers, the x variable and the y variables:
![\sqrt[3]{2\cdot16\cdot x^5\operatorname{\cdot}x^3\operatorname{\cdot}y^5\operatorname{\cdot}y^7}]()
The 16 we can write as its factors, and the variables we can put together using:
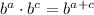
Doing so, we have:
![\sqrt[3]{2\cdot2^4\cdot x^(5+3)\cdot y^(5+7)}=\sqrt[3]{2^5x^8y^(12)}](https://img.qammunity.org/2023/formulas/mathematics/college/9qrqt7xsmwzlr6ymjb1ftthqd7hsuh2uwy.png)
Now, since the root is cubic root, for every 3 repetitions of a factor, we cancel it with the root.
So, for instance, we have 5 factors 2, so if we pick three of them, we can cancel with the cuibc root. We can do this to x and y too:
![\sqrt[3]{2^32^2x^3x^3x^2y^3y^3y^3y^3}=\sqrt[3]{2^3}\sqrt[3]{x^3}\sqrt[3]{x^3}\sqrt[3]{y^3}\sqrt[3]{y^3}\sqrt[3]{y^3}\sqrt[3]{y^3}\sqrt[3]{2^2x^2}=2\cdot x\cdot x\cdot y\cdot y\cdot y\cdot y\sqrt[3]{4x^2}=2x^2y^4\sqrt[3]{4x^2}](https://img.qammunity.org/2023/formulas/mathematics/college/e14gzznhnsucuvu1hvbzlj4q8d9k3kbivz.png)
So, the simplification becomes:
![\sqrt[3]{2x^5y^5}\cdot\sqrt[3]{16x^3y^7}=2x^2y^4\sqrt[3]{4x^2}](https://img.qammunity.org/2023/formulas/mathematics/college/y4h7l4zubzu20abipep8s4sgydob38fltq.png)