Given,
The angle of projection, θ=45°
The maximum horizontal distance the person can jump on earth, R_e=2.85 m
The acceleration due to the gravity of earth, g=9.80 m/s²
The acceleration due to gravity on the moon, g_m=g/6
The acceleration due to gravity on the mars, g_mr=0.38g
The maximum range of a projectile on earth is given by,

Where u is the maximum initial velocity with which the person can jump.
On substituting the known values,
![\begin{gathered} 2.85=(u^2)/(9.80) \\ u=\sqrt[]{2.85*9.80} \\ =5.28\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/kmp84obx3l5icq7e1ttl4z4sk958h9jwqz.png)
a)
The maximum range on the moon is given by,
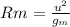
On substituting the known values,
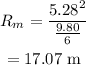
Thus the maximum range on the moon would be 17.07 m
b)
The maximum range on the mars is given by,
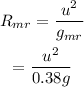
On substituting the known values,
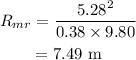
Thus the maximum range on the mars is 7.49 m