1 Answer

Diondra · Answer 1 · 2023-04-16T10:02:54+0000

We can solve this system by elimination method. We can take

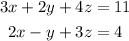
$\begin{gathered} 3x+2y+4z=11 \\ 2x-y+3z=4 \end{gathered}$

and multiply by 2 the second equation:

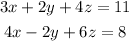
$\begin{gathered} 3x+2y+4z=11 \\ 4x-2y+6z=8 \end{gathered}$

and add both equations:

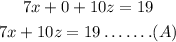
$\begin{gathered} 7x+0+10z=19 \\ 7x+10z=19\ldots\ldots.(A) \end{gathered}$

We can do something similar with 2nd and 3rd equations:

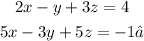
$\begin{gathered} 2x-y+3z=4 \\ 5x-3y+5z=-1 \end{gathered}$

but now, we can multiply by -3 the first one:

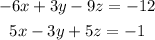
$\begin{gathered} -6x+3y-9z=-12 \\ 5x-3y+5z=-1 \end{gathered}$

by adding both equations, we have

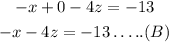
$\begin{gathered} -x+0-4z=-13 \\ -x-4z=-13\ldots..(B) \end{gathered}$

we have removed y, then we have equation A and B with only x and z varaibles:

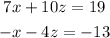
$\begin{gathered} 7x+10z=19 \\ -x-4z=-13 \end{gathered}$

by multiplying the second equation by 7 and adding to the first, we have

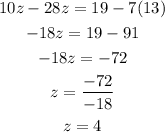
$\begin{gathered} 10z-28z=19-7(13) \\ -18z=19-91 \\ -18z=-72 \\ z=(-72)/(-18) \\ z=4 \end{gathered}$

Hence, we have that z=4. Now we can substitute tthis value into -x-4z=13 in order to find x:

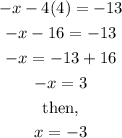
$\begin{gathered} -x-4(4)=-13 \\ -x-16=-13 \\ -x=-13+16 \\ -x=3 \\ \text{then,} \\ x=-3 \end{gathered}$

Finally, we can substitute x=-3 and z=4 into the first original equation in order to find y:

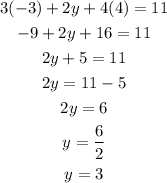
$\begin{gathered} 3(-3)+2y+4(4)=11 \\ -9+2y+16=11 \\ 2y+5=11 \\ 2y=11-5 \\ 2y=6 \\ y=(6)/(2) \\ y=3 \end{gathered}$

Hence, the solution is x=-3, y=3 and z=4.

Please log in or register to add a comment.