We can solve this system by elimination method. We can take
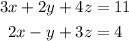
and multiply by 2 the second equation:

and add both equations:
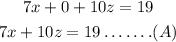
We can do something similar with 2nd and 3rd equations:

but now, we can multiply by -3 the first one:
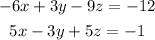
by adding both equations, we have
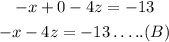
we have removed y, then we have equation A and B with only x and z varaibles:
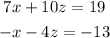
by multiplying the second equation by 7 and adding to the first, we have
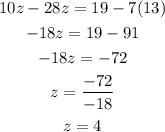
Hence, we have that z=4. Now we can substitute tthis value into -x-4z=13 in order to find x:
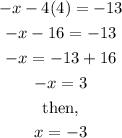
Finally, we can substitute x=-3 and z=4 into the first original equation in order to find y:
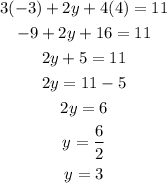
Hence, the solution is x=-3, y=3 and z=4.