Remember the following rules of exponents:
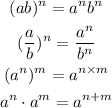
According to the third rule, all the exponents should have been multiplied by 4 rather than increasing them by 4 in the first step.
Therefore, the first incorrect step is Step 1, since all the exponents are increased by 4.