Question

Let f(x)=3x-7 and g(x)=x+6. Find f(gx)) and g(f(x)). Simplify your answer.

Answer 1

`\begin{gathered} f(x)=3x-7 \\ g(x)=x+6 \\ \\ \end{gathered}`

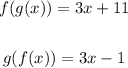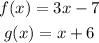
Composition of functions:

f(g(x)): Write the equation of f(x) and substitute the x in that equation by the equation of g(x):

`f(g(x))=3(x+6)-7`

Simplify:

`\begin{gathered} f(g(x))=3x+18-7 \\ \\ f(g(x))=3x+11 \end{gathered}`

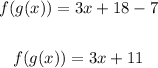
g(f(x)): Write the equation of g(x) and substitute the x in that equation by the equation of f(x):

`g(f(x))=(3x-7)+6`

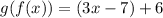
Simplify:

`\begin{gathered} g(f(x))=3x-7+6 \\ \\ g(f(x))=3x-1 \end{gathered}`

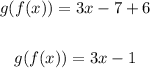
Then, the composition of the given functions is:
`\begin{gathered} f(g(x))=3x+11 \\ \\ g(f(x))=3x-1 \end{gathered}`