To solve this problem we first need to calculate the z-score of the sample:

Where x is the value we want to calculate the percent, the greek leter mu is the mean and the letter greek alpha is the standard deviation. For the first problem we have:
a.

We need to now check the z-table to find the percentage. In this case the percentage is:
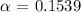
Which is the same as 15.39%.
b.
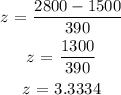
We need to check the z-table to find the percentage. In this case the percentage is:
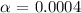
Which is the same as 0.04%
c.
Now the problem gaves us the percentile and we need to use:
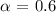
Checking at the z-table we have a z equal to z=0.255. We can now find the amount they would need to spend.

They would need to spend 1999.45