Question

Q=SYSTEMSClassifying systems of linear equations from graphsFor each system of linear equations shown below, dassify the system as "consistent dependent," "consistent independent," or "inconsistent." Then, choose thebest description of its solution. If the system has exactly one solution, give its solution.System ASystem BSystemLine 1:Line 1: Y:y= -4Line 1: y

Answer 1

To start, let's define consistent and inconsistent systems:

Cosistent Independent:

- Has one solution;

- The lines intercept at 1 point.

Consistent Dependent:

- Has Infinite solutions;

- The lines are the same.

Inconsistent:

- Has no solution;

The lines are parallel.

Now, let's evaluate each system.

System (A):

As we can observe in the graph, the lines are the same.

Also, you can isolate y in both equations to observe that the lines are the same:

Line 1:

`y=-(1)/(4)x-3`

Line 2:

`x+4y=-12`

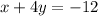
To isolate y in line 2, let's subtract x from both sides:

`\begin{gathered} x+4y-x=-12-x \\ 4y=-x-12 \end{gathered}`

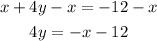
And now divide both sides by 4:

`\begin{gathered} (4y)/(4)=(-x-12)/(4) \\ y=-(1)/(4)x-3 \end{gathered}`

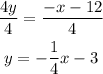
As can be observed, Line 1 and 2 are the same.

So, the system is consistent dependent.

This means that the system has Infinite solutions.

System (B):

As we can observe in the graph, the lines are parallel.

Also, comparing the equations, observe that they have the same angular coefficient but different intercepts, confirming that the lines are parallel.

So, the system is inconsistent.

This means that the system has no solutions.

System (C):

As we can observe in the graph, the lines intercept at one point.

So, let's find the intercept.

Do y1 = y2:

`\begin{gathered} y_1=y_2 \\ -(1)/(2)x-3=x \end{gathered}`

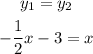
Now, isolate x by adding 1/2x to both sides.

`\begin{gathered} -(1)/(2)x-3+(1)/(2)x=x+(1)/(2)x \\ -3=(2x+x)/(2) \\ -3=(3)/(2)x \end{gathered}`

Now, multiply both sides by 2/3:

`\begin{gathered} -3\cdot(2)/(3)=(3)/(2)x\cdot(2)/(3) \\ -(6)/(3)=(6)/(6)x \\ -2=x \end{gathered}`

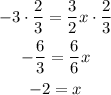
Knowing x, substitute it in one equation to find y. In Line 2 x = y. Then,

`\begin{gathered} x=y \\ \text{If x = -2} \\ -2=y \end{gathered}`

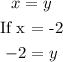
Thus, the intercept is (-2, -2).

So, the system is consistent independent.

This means that the system has a unique solution. The solution is (-2, -2).