Question

Solve.3x+y=42x+y=5Use the linear combination method. (−3, 13)(−3, 12)(0, 4)(−1, 7)

Answer 1

We have the following system of equations:

`\begin{gathered} 3x+y=4 \\ 2x+y=5 \end{gathered}`

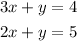
The linear combintation method is a process of adding two algebraic equations so that one od the variables is eliminated.

In this regard, by multiplying the second equation by -1, we obtain an equivalent system of equations:

`\begin{gathered} 3x+y=4 \\ -2x-y=-5 \end{gathered}`

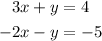
Then, by adding both equations, we can eliminate the variable y, that is,

`\begin{gathered} 3x-2x+y-y=4-5 \\ \text{which gives} \\ x=-1 \end{gathered}`

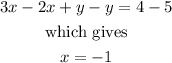
Once we know the result for x, we can substitute its values into one of the orginal equations. Then, if we substitute x=-1 into the first equation, we have

`3(-1)+y=4`

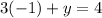
which gives

`\begin{gathered} -3+y=4 \\ \text{then} \\ y=7 \end{gathered}`

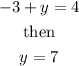
Therefore, the solution is ( -1, 7), which corresponds to the last option.