Given:
Mass of sphere 1 = m
Speed of sphere 1 = υ
Mass of sphere 2 = 2m
Speed of sphere 2 = -υ
In a system of colliding bodies, the final kinetic energy is less than the initial kinetic energy of the system.
Let's determine the kinetic energy before and after collision using the formula:
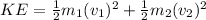
Thus, we have:
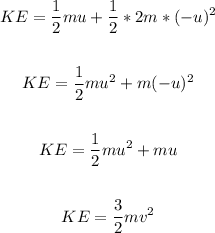
Therefore, the kinetic energy of the system both before and after impact is 3/2 mv².
ANSWER:
c). The kinetic energy of the system both before and after the impact is equal with 3/2 mv².