From the diagram provided, the line segment WZ represents the radius of the circle. That means,
R = 5.3
Also, note that

Next, observe that the angle formed by arc VW at VZW lies on a straight line with angle 108. Therefore,
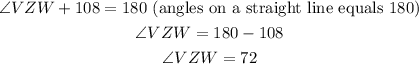
Also, arc VW equals arc XY, since both arcs are subtended by the same angle. Angle VZW and angle XZY are vertically opposite angles. Therefore we now have;
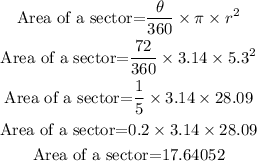
Note that there are two similar shaded sectors. Therefore the area of the shaded sectors equals;
Area = 17.64052 x 2
Area = 35.28104
Area = 35.28 km squared (rounded to the nearest hundredth)