Given:
margin of error = 10% or 0.10 in decimal form
confidence level = 95%
Find: sample size
Solution:
To determine the sample size, we can use Cochran's formula.
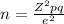
where:
Z is the critical value of the given confidence level
p = estimated proportion of the population having the attribute in question (ex. supports the candidate)
q = 1 - p
e = margin of error
Based on the given information, our confidence level is 95%. The z-value at this confidence level is 1.96. Hence, z = 1.96.
For p and q, since none is stated in the question, we will assume p = 0.5 and q = 0.5 or 50% each.
Let's plug into the formula above the values of Z, p, q, and e.
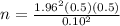
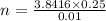

Any excess decimal will be considered as 1 person. So, 96 + 1 = 97.
Therefore, we need 97 people as our sample size.