Question

Which of the following gives the correct intercept points and vertex point for the function f(x) = x2 + 5x + 6?

Answer 1

We are given the following quadratic equation.

`f(x)=x^2+5x+6`

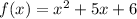
Recall that the standard form of a quadratic equation is given by

`f(x)=ax^2+bx+c`

Comparing the given equation with the standard form, the coefficients are

a = 1

b = 5

c = 6

The vertex point is given by

`h=-(b)/(2a)=-(5)/(2(1))=-(5)/(2)`
`\begin{gathered} f(-(5)/(2))=(-(5)/(2))^2+5(-(5)/(2))+6 \\ f(-(5)/(2))=(25)/(4)^{}-(25)/(2)+6 \\ f(-(5)/(2))=-(1)/(4) \end{gathered}`

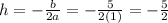
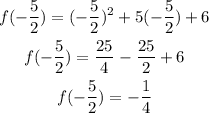
So, the vertex point is

`vertex\: point=(-(5)/(2),-(1)/(4))`

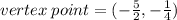
Now let us find the y-intercept of this equation.

Substitute x = 0 into the equation

`\begin{gathered} f(x)=x^2+5x+6 \\ f(0)=0^2+5(0)+6 \\ f(0)=6 \end{gathered}`

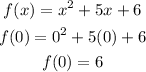
So, the y-intercept is

`y-intercept=(0,6)`

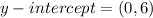
Finally, let us find the x-intercept of this equation

Substitute f(x) = 0 into the equation

`\begin{gathered} 0=x^2+5x+6 \\ 0=x^2+3x+2x+6 \\ 0=x(x+3)+2(x+3)_{} \\ 0=(x+2)\mleft(x+3\mright)_{} \\ (x+2)=0\: \: and\: \: (x+3)=0\: _{} \\ x=-2\: \: and\: \: x=-3 \end{gathered}`

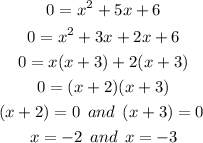
So, the x-intercepts are

`x-intercepts=(-2,0)\: and\: (-3,0)_{}`

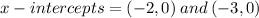
Conclusion:

`y-intercept=(0,6)\quad vertex\: point=(-(5)/(2),-(1)/(4))\quad x-intercepts=(-2,0)\: and\: (-3,0)_{}`

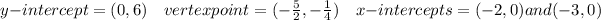
Therefore, the correct answer is option B