Question

Mitch and Bill are both age 75. When Mitch was 24 years old, he began depositing $1,000 per year into a savings account. He made deposits for the first 10 years, at which point he was forced to stop making deposits. However, he left his money in the account, where it continued to earn interest for the next 41 years. Bill didn't start saving until he was 45 years old, but for the next 30 years he made annual deposits of $1,000. Assume that both accounts earned an average annual return of 5% (compounded once a year).a. How much money does Mitch have in his account at age 75?b. How much money does Bill have in his account at age 75?Mitch deposits $___in his account and Bill deposits $____ in his account.Draw a conclusion about this parable. Choose the correct answer below.A.Bill ends up with more money in his account than Mitch because he make more deposits than Mitch, and each additional deposit will accrue interest each year.B.Mitch ends up with more money in his account despite not having deposited as much money as Bill because the interest that is initially accumulated accrues interest throughout the life of the account.C.Both Bill and Mitch have the same return on their investments despite using different methods of saving.D.Both Bill and Mitch end with the same amount of money in their accounts, but Mitch had to deposit less money using his method. It is better to start saving as early as possible.

Answer 1

The compounded interest formula to calculate the final values is:

`V_f=V_i(1+i)^n`

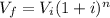
Now calculate the balance of the Mitch account at age of 34 (first 10 years)

`A=1000*((1+0.05)^(10)-1)/(0.05)=12577.89`

In the first 10 years, Mitch accumulate $12,577.89

Now calculate the future value for the compound interest formula for the next 41 years.

`V_f=12577.89(1+0.05)^(41)=92975.63`

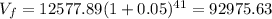
So Mitch has in his account at age of 75 $92975.63

Now calculate the balance for the Bill account after 30 years of deposits:

`A=1000*((1+0.05)^(30)-1)/(0.05)=66438.85`

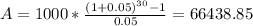
So Bill has $66,438.85 at age of 75.

Remember that Mitch deposits $10,000 ($1,000*10years) and Bill deposits $30,000 ($1,000*30years)

The final answer and conclusion are:

B.

Mitch ends up with more money in his account despite not having deposited as much money as Bill because the interest that is initially accumulated accrues interest throughout the life of the account.