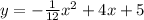
when the ball leaves the chil'd hand the distance is 0
so:
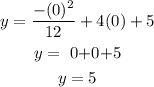
the height is 5 feets
The maximun height happens when x=-b/(2a) because is the vertex
where b=4 and a=-1/12
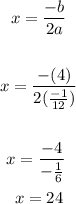
so x is the distance where maximun height happens, so replace on the function
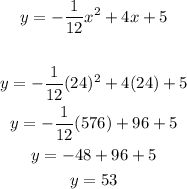
the maximun height is 53 feets
the ball strike the ground when the height is 0 so we can replace y and fin x or the distance

we need to factor and we can do it with this equation
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
where a= -1/12 , b=4 and c=5
![\begin{gathered} x=\frac{-(4)\pm\sqrt[]{(4)^2-4(-(1)/(12))(5)}}{2(-(1)/(12))} \\ \\ x=\frac{-4\pm\sqrt[]{16+((5)/(3))}}{-(1)/(6)} \\ x=-6(-4\pm\sqrt[]{(53)/(3)}) \\ \\ x=-6(-4\pm4.20) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/qshbgq5xcaq4b9l4hmgo6g9frcr76rt3gm.png)
we have 2 solutions
1.
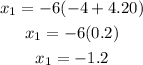
but its not a real solution because distance cant be negative
2.
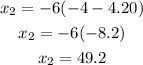
so the distance when the ball strike the ground is 49.2 feets