ANSWER
It will take 13 years.
Step-by-step explanation
First, we have to write the equation that represents the situation.
It is a depreciation, which means that it is a compound decrease.
Compound decrease is generally given as:

Therefore, from the question:
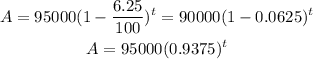
To find the number of years after which the boat will have a value of $40,000, we have to find t when A is $40,000.
That is:

It will babout 13 years for the value for the value of the car to be $40,000.