Given,
The height difference, h=1.23 m
The blood pressure at the aorta, P₁=104 mmHg
The density of the blood, ρ=1060 kg/m³
From Pascal's law, the pressure difference is given by,
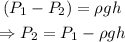
Where P₂ is the required pressure and g is the acceleration due to gravity.
Let us calculate the value of ρgh as it will be in the pascal.
On substituting the known values,
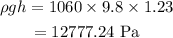
On converting it to mmHg,
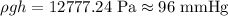
Therefore the pressure in a person's foot is,
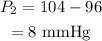
Therefore the average blood pressure in a person's foot is 8 mmHg