Question

Not yet answeredMarket out of 1.00 Nas questionThere is a bank which offers a 0.8% yearly interest rate compounding monthly. You put$1000 into this bank and then withdraw your money 25 years later. How much money is inyour account after 25 years?

Answer 1

Given:

Principal, P= $1000

Interest rate, r = 0.8% = 0.008

Number of years, n = 25 years

To find the amount of money after 25 years, use the compound interest formula below.

`A\text{ = }P(1+r)^n`

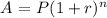
Thus, we have:

`A\text{ = }1000(1+0.008)^(25)`
`\begin{gathered} A=1000(1.008)^(25) \\ \\ \text{ = 1000}(1.22043) \\ \text{ = 1220}.43 \end{gathered}`

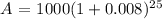
Therefore, the amount of money in the account after 25 years is $1,220.43

ANSWER:

$1,220.43