Question

In ΔBCA, BA = 17 cm, BF = 6 cm, CG = 9 cm. Find the perimeter of ΔBCA.

Answer 1

Answer: 52 cm

Hope this helps!

Stay safe, stay happy, and remember to have a great day!

-ishaqrocks8

Proof is below:

Answer 2

To solve this problem we will use the rule

The 2 tangents drawn from a point outside the circle are equal in length

From the given picture we can see

A circle D is inscribed in the triangle ABC and touches its sides at points H, F, and G

By using the rule above

AH = AG

BH = BF

CF = CG

Since BF = 6 cm, then BH = 6cm

Since CG = 9 cm, then CF = 9 cm

Since AB = 17 cm

Since AB = BH + HA

Since BH = 6 cm, then

`17=6+HA`

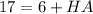
Subtract 6 from both sides

`\begin{gathered} 17-6=6-6+HA \\ 11=HA \end{gathered}`

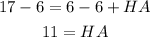
Since HA = AG, then AG = 11 cm

Now, we can find the length of BC and AC

`\begin{gathered} BC=BF+FC \\ BC=6+9 \\ BC=15\text{ cm} \end{gathered}`
`\begin{gathered} AC=AG+GC \\ AC=11+9 \\ AC=20\text{ cm} \end{gathered}`

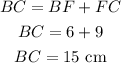
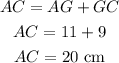
Since the perimeter of the triangle = the sum of the lengths of its sides, then

`\begin{gathered} P=17+15+20 \\ P=52\text{ cm} \end{gathered}`

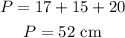
The answer is the 1st choice