To solve this problem we will use the rule
The 2 tangents drawn from a point outside the circle are equal in length
From the given picture we can see
A circle D is inscribed in the triangle ABC and touches its sides at points H, F, and G
By using the rule above
AH = AG
BH = BF
CF = CG
Since BF = 6 cm, then BH = 6cm
Since CG = 9 cm, then CF = 9 cm
Since AB = 17 cm
Since AB = BH + HA
Since BH = 6 cm, then
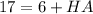
Subtract 6 from both sides
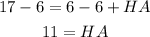
Since HA = AG, then AG = 11 cm
Now, we can find the length of BC and AC
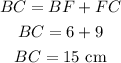
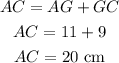
Since the perimeter of the triangle = the sum of the lengths of its sides, then
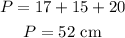
The answer is the 1st choice