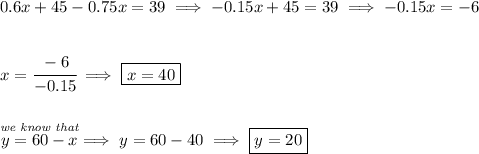we know that A has 60% of salt, so if way we had "x" amount of ounces of A solution the amount in it will be 60% of "x", or namely (60/100)*x = 0.6x.
Likewise for solution B if we had "y" ounces of it, the amount of salt in it will be (75/100) * y or 0.75y, thus