Question

IQ test scores are standardizeddistribution with a mean of μ=100 and a standarddeviation of o=15. Find the proportion of the population in each of the following IQ categories.a. Average or normal intelligence: IQ from 90 to 109

Answer 1

Hello there. To solve this question, we have to remember some properties about statistics.

We want to determine the proportion of the population in each of the following IQ categories knowing that IQ score tests are standardized distribution with mean μ=100 and a standard deviation of o=15.

a) Average or normal intelligence: IQ from 90 to 109

For this, we want to determine

`P(90\leq X\leq109)`

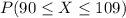
Now, we have to normalize these values doing the transformation:

`Z=(X-\mu)/(\sigma)`

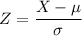
Hence we plug the values for the mean and standard deviation of the population:

`\begin{gathered} P\left((90-100)/(15)\leq\right.(X-100)/(15)\leq(109-100)/(15)\biggr) \\ \\ \Rightarrow P(-0.67\leq Z\leq0.6) \end{gathered}`

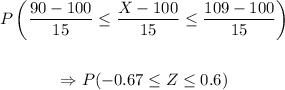
Using the properties for probabilities, thinking of it as the following left accumulated area:

It is the same as the difference between: