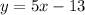Question

Pick a nonzero number m for a slope and a point in the plane. Find an equation of the line with the chosen slope that passes through the chosen points.

Answer 1

The equation of a line passing through a point X having its coordinates to be (x₁, y₂) is given as

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{where} \\ m\text{ is the slope of the line} \\ (x_(1,)y_1)\text{ is the coordinate of the point X} \end{gathered}`

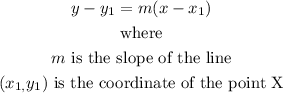
Taking a nonzero number for the slope m and a point in the plane,

`\begin{gathered} \text{let} \\ m=5 \\ (x_(1,)y_1)\text{ = (3,2)} \end{gathered}`

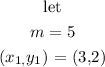
Thus, the equation of the line becomes

Hence, the equation of the line with the chosen slope (5) passing through the chosen point (3,2) is evaluated to be

`y=5x-13`