Let 'x' represents the advance ticket,
Let 'y' represents the same-day ticket.
Therefore,
The combined cost of one advance ticket and the same ticket is $60, and it can be represented mathematically below.
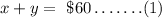
Secondly, the sum of 25 advance tickets and 40 same-day tickets is $2025. Mathematically,
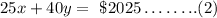
Let us now combine the equations together,
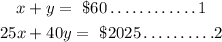
Let us make x the subject of the formula in equation (1),
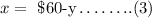
Now let us substitute the 'x' into equation (2), and solve for y.
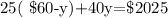
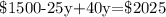
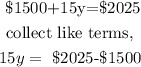
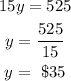
Let us now substitute the value of y into equation 3 to solve for x,
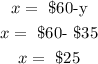
Hence, Advance ticket is $25,
Same-day ticket is $35.