Question

and $7 for children. The dance company sold 253 tickets, and the total receipts were $2,771. How many adult tickets and how many child tickets were sold?

Answer 1

Let the number of adult tickets sold be x

and the number of child tickets sold be y

Given:

Cost of tickets for adults = $15

Cost of tickets for children = $7

Total number of tickets sold = 253

Total receipts = $ 2771

Solution

The sum of the number of adults and child tickets is:

`x\text{ + y = 253}`

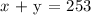
The receipt for adults :

`=\text{ 15x }`

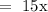
The receipts for children:

`=\text{ 7y}`

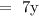
The sum of the receipts for adults and children is the total receipts:

`15x\text{ + 7y = 2771}`

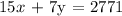
Solving the equations simultaneously, we can obtain x and y:

`\begin{gathered} x\text{ + y = 253} \\ 15x\text{ + 7y = 2771} \end{gathered}`

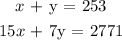
The values of x and y after solving simultaneously are :

`\begin{gathered} x\text{ = 125} \\ y\text{ = 128} \end{gathered}`

Answer: The number of adults tickets = 125

The number of child tickets = 128