Let the number of adult tickets sold be x
and the number of child tickets sold be y
Given:
Cost of tickets for adults = $15
Cost of tickets for children = $7
Total number of tickets sold = 253
Total receipts = $ 2771
Solution
The sum of the number of adults and child tickets is:
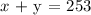
The receipt for adults :
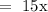
The receipts for children:
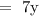
The sum of the receipts for adults and children is the total receipts:
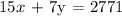
Solving the equations simultaneously, we can obtain x and y:
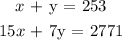
The values of x and y after solving simultaneously are :
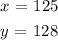
Answer: The number of adults tickets = 125
The number of child tickets = 128