By definition, when the line cuts the x-axis, the value of "y" is:

Therefore, to find the x-intercept of the line given in the exercise, you must substitute that value of "y" into the equation and solve for "x":

The equation of a line in Slope-Intercept form is:

Where "m" is the slope and "b" is the y-intercept.
Kwnowing that the line is:
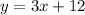
You can identify that the y-intercept is:

So, you have these points:
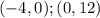
The formula used to find the distance between two points, is:
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/be685jmxw05hm2tq94m5iuge2xjynn1hfn.png)
In this case:
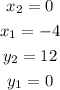
Substituting values and evaluating, you get that the distance between the y-intercept and x-intercept of the line, is:
![d=\sqrt[]{(0-(-4))^2+(12-0)^2}=\sqrt[]{16+144}=\sqrt[]{160}](https://img.qammunity.org/2023/formulas/mathematics/college/9fnjssz7oc5qgsmvluiqne8yxja6bjpvkz.png)
The answer is the option (2).