A linear function is shown below. Choose the two points that are on the graph of the inverse of this function. A- (-1,4)B (2 , -6)C ( 2, -2)D ( 1, 0)E ( 0 , -1 ) F ( -4 , 3)

Question

asked Nov 21, 2023 44.0k views

1 Answer

Samnu Pel · Answer 1 · 2023-11-26T04:35:20+0000

First, we need to find the function of the line.

Use two points of the line to find the slope:

Let us choose (- 1, 0) and E ( 0 , -2) :

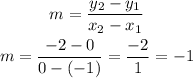
$\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(-2-0)/(0-(-1))=(-2)/(1)=-1 \end{gathered}$

Then, the slope=m=1.

Now, we can find the equation using:

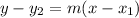
Replace using m=-2and P1(-1,0)

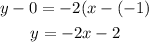
$\begin{gathered} y-0=-2(x-(-1) \\ y=-2x-2 \end{gathered}$

To find the inverse function, we need to solve for x:

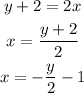
$\begin{gathered} y+2=2x \\ x=(y+2)/(2) \\ x=-(y)/(2)-1 \end{gathered}$

Interchange x and y:

Hence, the inverse function is:

When =

$\begin{gathered} y=0+1 \\ y=1 \end{gathered}$

Now, we need to find two points for the graph of the inverse function.

When x=0:

$\begin{gathered} y=-(0)/(2)-1 \\ y=-1 \end{gathered}$

We found the point (0,-1)

When x=2

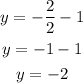
$\begin{gathered} y=-(2)/(2)-1 \\ y=-1-1 \\ y=-2 \end{gathered}$

We found the point (2,-2)

Hence, the correct answers are options C and E.