Answer:
Concept:
Two vectors a and b are orthogonal if they are perpendicular, i.e., the angle between them is 90° (Fig. ... Condition of vectors orthogonality. Two vectors a and b are orthogonal if their dot product is equal to zero.
The dot product of two vectors will be calculated using the formula below
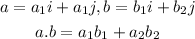
The vectors are given below as
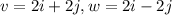
By applying the principle, we will have
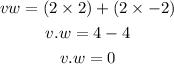
Hence,
They are orthogonal because the dot product is = 0
The final answer is OPTION A