Question

-Use the dot product to determine whether v and w are orthogonal.v = 2i +2j, w = 2i - 2jSelect the correct choice below and, if necessary, fill in the answer box to complete your chO A. They are orthogonal because the dot product isO B. They are not orthogonal because the dot product is

Answer 1

Concept:

Two vectors a and b are orthogonal if they are perpendicular, i.e., the angle between them is 90° (Fig. ... Condition of vectors orthogonality. Two vectors a and b are orthogonal if their dot product is equal to zero.

The dot product of two vectors will be calculated using the formula below

`\begin{gathered} a=a_1i+a_1j,b=b_1i+b_2j \\ a.b=a_1b_1+a_2b_2 \end{gathered}`

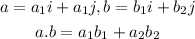
The vectors are given below as

`v=2i+2j,w=2i-2j`

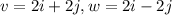
By applying the principle, we will have

`\begin{gathered} vw=(2*2)+(2*-2) \\ v\text{.}w=4-4 \\ v.w=0 \end{gathered}`

Hence,

They are orthogonal because the dot product is = 0

The final answer is OPTION A