The translation of functions can be determined by the structure of the function. In the case of an exponential function, the general structure is:
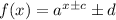
if we look at the exponent there is an addition or subtraction depending on the sign, if the sign is positive then the graph moves c units to the left, if the sign is negative then the graph moves c units to the right, in this case, the exponent is being added 3 units, this means the graph moves 3 units to the left.
Now, if we look at the complete function there is an addition or subtraction depending on the sign, if the sign is positive then the graph moves d units upward, if the sign is negative then the graph moves d units downward, in this case, the function is being added 2 units, meaning the graph moves 2 units upward.
the blue line represents the parent function, and the red line represents the translation of the function
Answer: