Given:
The total number of jeans is, j = 2.
The cost of jeans is, c (j) = $60.
The cos of t shirts is, c (t) = $12.
The total budjet of the purchase is, T = $130.
The objective is to find the maximum number of t-shirts that can be buy.
Explanaion:
Consider the number of t-shirts as t.
Then, the equation of cost can be written as,
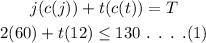
To find t :
On solving the equation for t,
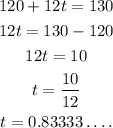
Since the value of t-shirt is less than 1, the person cannot buy any t-shirt.
Hence, the maximum number of t-shirts that can be buy with a budjet of $130 is zero.