Question

The rate at which a certain balloon travels is inversely proportional to the amount of weight attached to it. If the balloon travels at 10 inches per second when there is a 2-gram weight attached to it, approximately how much weight must be attached to the balloon for it to travel 18 inches per second?

Answer 1

Given Data:

The rat travels 10 in/sec when 2 grams is attached.

Since the distance tarved and the weight are in inversely propotional, it can be written as,

`d=(k)/(W)`

Here, k is a proportionality constant, and W is the weight added.

When 2 gram added the rat traveled 10 in/sec.

`\begin{gathered} d=(k)/(W) \\ 10=(k)/(2) \\ k=10*2 \\ k=20 \end{gathered}`

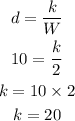
If the rate traveled 18 in/sec the weight added is,

`\begin{gathered} d=(k)/(W) \\ 18=(k)/(W) \\ W=(k)/(18) \end{gathered}`

Substitute value of k in the above expression.

`\begin{gathered} W=(20)/(18) \\ =(10)/(9) \\ =1.11\text{ gram.} \end{gathered}`

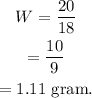
Thus, the rat travels 18 in/sec when added 1.1 grams of weight.