Given Data:
The rat travels 10 in/sec when 2 grams is attached.
Since the distance tarved and the weight are in inversely propotional, it can be written as,
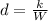
Here, k is a proportionality constant, and W is the weight added.
When 2 gram added the rat traveled 10 in/sec.
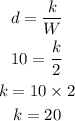
If the rate traveled 18 in/sec the weight added is,
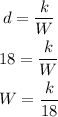
Substitute value of k in the above expression.
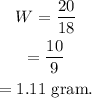
Thus, the rat travels 18 in/sec when added 1.1 grams of weight.