Question

In F(x)=2x-4/x(x^2-4) which are non removable ?

Answer 1

Ok, so

Here we have the following function:

`F(x)=(2x-4)/(x(x^2-4))`

We want to check if the discontinuity of F(x) is removable or non removable.

We could factor the expression in the denominator using the following property:

`a^2-b^2=(a+b)(a-b)`

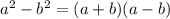
And we could apply the common factor property in the numerator.

Then,

`\begin{gathered} (2x-4)/(x(x^2-4)) \\ \\ (2(x-2))/(x(x+2)(x-2)) \end{gathered}`

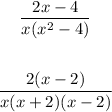
We can cancel the "x-2" term.

In the above expression due to (x-2) in the denominator, f(x) becomes undefined at x=2, Hence there is a discontinuity at x=2. However this (x-2) gets cancelled by (x-2) in the numerator, and we obtain:

`(2)/(x(x+2))`

Notice that the new expression has a discontinuity at the points x=0 and x=-2. For this reason, there is a non removable discontinuity at x=0 and x=-2, because the function becomes undefined at these points and there's not a way to cancel them.