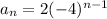EXPLANATION
Geometric Progression:
A geometric sequence has a constant ratio r and is defined by:
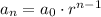
Check wheter the ratio is constant: r=-4
2, -8 , 32, -128
Compute the ratios of all the adjacent terms:
-8/2= -4, 32/-8=-4, -128/32=-4
The ratio of all the adjacent terms is the same and equal to:
r=-4
The first element of the sequence is:
a_1=2
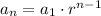
Therefore, the nth term is computed by
r=-4,