The ratio between the lengths of 2 rectangles is the same between their perimeters
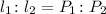
Since the ratio between the length of rectangle A and the length of rectangle B is 7: 3, then
The ratio between the perimeter of rectangle A to the perimeter of rectangle B is 7: 3 too

Since the perimeter of rectangle A is 540, then
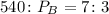
We will write them as a fraction
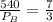
By using the cross multiplication
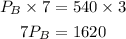
Divide both sides by 7

Round it to the nearest tenth
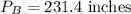
The perimeter of the smaller rectangle B is 231.4 inches