Question

Finding a specified term of a geometric sequence given to terms of the sequence

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given parameters

`\begin{gathered} a_6=ar^5=(17)/(625) \\ a_(11)=ar^(10)=-85 \\ where\text{ a is the first term and r is the common ratio} \end{gathered}`

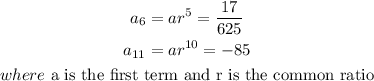
STEP 2: Divide the two expressions to get the common ratio

`\begin{gathered} (a_(11))/(a_6)=(ar^(10))/(ar^5)=-(85)/((17)/(625)) \\ a\text{ cancels a} \\ r^(10-5)=-85/(17)/(625) \\ r^5=-85*(625)/(17)=-5*625=-3125 \\ r=\sqrt[5]{-3125}=-5 \\ common-ratio=-5 \end{gathered}`

STEP 3: Get the first term

`\begin{gathered} From\text{ equation in step 1,} \\ ar^5=(17)/(625) \\ By\text{ substitution,} \\ a(-5)^5=(17)/(625) \\ a*-3125=(17)/(625) \\ Divide\text{ both sides by -3125} \\ a=(17)/(625)/-3125=(17)/(625)*(1)/(-3125) \\ a=-(17)/(1953125) \end{gathered}`

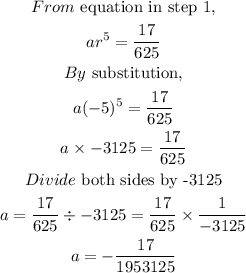
STEP 4: Calculate the 14th term

`\begin{gathered} a_(14)=ar^(13) \\ a_(14)=-(17)/(1953125)*-5^(13) \\ a_(14)=10625 \end{gathered}`

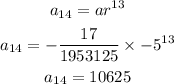
Hence, the 14th term is 10625