The given information is:
- The tank has the shape of a cylinder
- The dimensions of the cylinder are 5 ft long and diameter 2.2 ft.
- The tank is drained at a rate of 2.1 ft^3 per minute.
The volume of the tank is given by the formula:
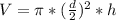
Where d is the diameter and h is the height.
By replacing the known values we obtain the initial volume:
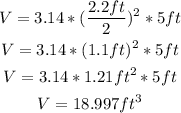
As the drain rate is 2.1 ft^3 per minute, the time that is needed to empty the tank is:
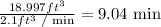
The answer is 9 minutes.